3.8 Otras Aplicaciones

— Aplicación del límite y la derivada a la determinación e interpretación
de las propiedades locales de funciones habituales
basadas en situaciones contextualizadas.
— Aplicación del cálculo de derivadas elementales (polinómicas,
exponenciales y logarítmicas, productos y cocientes) a problemas
de optimización. Estudio y representación gráfica de
funciones a partir de sus propiedades globales.
— Aproximación intuitiva al concepto de integral definida: El
problema del cálculo del área limitada por una curva.
Estadística y probabilidad:
— Profundización en los conceptos de probabilidades compuestas,
condicionadas, totales y a posteriori. Utilización de técnicas
elementales (conteo directo, diagrama en árbol...).
— Introducción al concepto, uso y alcance de la inferencia estadística:
Problemas relacionados con la elección de las muestras,
las condiciones de representatividad y análisis de las
conclusiones que cabe extraer de ellas.
— Estudio de algún test de contraste de hipótesis basado en la
distribución normal y aplicación a situaciones sencillas.
Criterios de evaluación
— Utilizar el lenguaje matricial y aplicar las operaciones con
matrices como instrumento para el tratamiento de situaciones
que manejen datos estructurados en forma de tablas o grafos.
— Transcribir un problema expresado en lenguaje usual al lenguaje
algebraico y resolverlo utilizando técnicas algebraicas
determinadas: Matrices, resolución de sistemas de ecuaciones
y programación lineal bidimensional.
— Analizar cualitativa y cuantitativamente las propiedades locales
(límites, crecimiento, derivadas, máximos y mínimos) de una
función que describa una situación real, extraída de fenómenos
habituales en las ciencias sociales.
— Utilizar el cálculo de derivadas como herramienta para resolver
problemas de optimización extraídos de situaciones reales de
carácter económico y sociológico.
— Asignar e interpretar probabilidades a sucesos aleatorios
simples y compuestos (dependientes o independientes) utilizando
técnicas de conteo directo, diagramas de árbol o cálculos
simples.
— Analizar informes estadísticos dados, detectando posibles
errores y manipulaciones en la presentación de determinados
datos.
Opción 6. Familia Profesional: Comunicación, Imagen y Sonido
Física
Contenidos
Vibraciones y ondas:
— Movimiento oscilatorio: El movimiento vibratorio armónico
simple.
— Movimiento ondulatorio. Magnitudes y características de las
ondas. Estudio fenomenológico de la influencia del medio en
la velocidad de propagación. Ecuación de las ondas armónicas.
Aplicaciones.
— Estudio cualitativo de algunas propiedades de las ondas: Reflexión,
refracción, difracción e interferencias. Principios de
Huygens. Ondas estacionarias.
— Contaminación sonora, sus fuentes y efectos.
Óptica:
— Controversia sobre la naturaleza de la luz: Análisis de losmodelos
corpuscular y ondulatorio e influencia de los factores
extracientíficos en su aceptación por la comunidad científica.
— Dependencia de la velocidad de la luz con el medio. Algunos
fenómenos producidos con el cambio de medio: Reflexión,
refracción, absorción y dispersión.
— Óptica geométrica: Comprensión de la visión y formación de
imágenes en espejos y lentes delgadas. Aplicación al estudio
de algún sistema óptico.
— Estudio cualitativo y experimental de los fenómenos de difracción,
interferencias, dispersión y espectro visible.
— Aplicaciones: Visión del color y espectroscopia.
Interacción electromagnética:
— Campo eléctrico. Magnitudes que lo caracterizan: Intensidad
de campo y potencial eléctrico. Relación entre ellas.
— Creación de campos magnéticos por cargas en movimiento.
Estudio experimental de algunos casos concretos: Campos
creados por una corriente rectilínea indefinida y por un solenoide
en su interior. Explicación del magnetismo natural.
— Fuerzas sobre cargas móviles situadas en campos magnéticos:
Ley de Lorentz. Aplicación al estudio del movimiento de
cargas eléctricas en campos magnéticos uniformes. Definición
internacional de amperio.
— Flujo magnético. Producción de corrientes alternas mediante
variaciones del flujo magnético: Inducción electromagnética.
Importancia de su producción e impacto ambiental.
— Aproximación histórica a la utilización de la electricidad, el
magnetismo y la óptica: Síntesis electromagnética.
— Analogías y diferencias entre distintos campos conservativos
(gravitatorio y eléctrico), y entre conservativos y no conservativos
(eléctrico y magnético).
Criterios de evaluación
— Deducir a partir de la ecuación de ondas las magnitudes que
las caracterizan y asociar dichas características a su percepción
sensorial.
— Justificar algunos fenómenos ópticos sencillos de formación
de imágenes, y representar alguno de ellos.
— Utilizar el concepto de campo para superar las dificultades
que plantea la interacción a distancia, calcular los campos
creados por cargas y corrientes y las fuerzas que actúan sobre
cargas y corrientes en el seno de campos uniformes, y justificar
el fundamento de algunas aplicaciones prácticas.
Imagen
Contenidos
Imagen fija:
— Fotografía. El campo visual. El enfoque y la superposición.
La aplicación de la fotografía en la elaboración de un mensaje,
a través de los distintos modos de lenguaje. El fotomontaje.
Estrategias visuales.
— Imágenes generadas por ordenador. Captación y transformación
de imágenes. Fabricación de imágenes a través de programas
específicos. Intercambio de imágenes vídeo-ordenador.
Aplicaciones gráficas del ordenador: Diseño gráfico, ilustración,
cine y televisión, ciencia, industria, negocios.
— Diaporama: Diapositivas a mano y con cámara. Estructuración.
Preparación de diapositivas. Utilización del proyector.
Diaporama con dos o más proyectores. Unidad de fundido.
Composición con imágenes fundidas o con imágenes adosadas.
— Cómic. Análisis Preiconográfico: Análisis iconográfico.
Análisis iconológico. Estructuración gráfica: Predominio
sincrónico o didáctico, ritmo y secuencias cambiantes, códigos
cinéticos, códigos gestuales. La viñeta y el globo. Delta
y estilema.
— Fotonovela: Guión literario, secuenciación fotográfica. Montaje
y distribución, imagen-texto.
— Publicidad gráfica. Imagen y palabra. El color en la publicidad.
Medios: Publicidad exterior, publicidad en lugar de ventas,
prensa y revistas, impresos. Objetivos de la publicidad.
— Copy-art. Toma directa. Efectos con diferentes soportes.Modelos
corporales. Retratos. Procesos degenerativos. Reentintados.
Superposiciones. Fotocopias al vaciado. El “collage”.
Aplicaciones al diseño y maquetación. Producción seriada.
Imagen en movimiento:
— Dibujos animados. El lenguaje de la animación, técnicas de
animación. Animación por ordenador. Animación en cine.
Animación en vídeo.
— Cine. Guión literario. Guión técnico. “Story board”. Unidades
de narración: Plano, escena, secuencia. Tipos de plano utilizados.
Movimientos de la cámara. Ángulos de toma. Signos
de puntuación y tiempo. Equipos de realización. Materiales.
— Vídeo. Guión literario. Guión técnico. Manejo de la cámara.

Evaluacion Parcial 4.2-4.7

Por medio de la presente manifiesto una disculpa por no haber publicado antes su evaluacion ya que obtuvo el 100% de los subtemas 4.2 al 4.7.

Atentamente
Ing. Jose Enrique Marquez E

4.1 Definicion de serie: 4.1.1 Finita, 4.1.2 Infinita (Criterio de D' Alembert) (Criterio de Cauchy)

4.1 Definicion de serie
Definiciones y notación.

A la suma de una sucesión de términos se denomina SERIE y el valor de dicha suma, si es que tiene
alguno, se define como

S = lim S n .
n→∞
Un ejemplo de serie infinita, denominada así debido a que dicha sucesión es infinita, es la
denominada serie geométrica, la cual se obtiene a partir de un térmno inicial
multiplicado por una cantidad constante, p. ej.
a + ar + ar 2 + ar 3 + ⋅ ⋅ ⋅ + ar n −1 + ⋅ ⋅ ⋅ . En
este caso la cantidad inicial a es multiplicada por la cantidad constante r para obtener dicha
serie infinita.
En general una serie infinita significa una expresión de la forma
a1 + a2 + a3 + ⋅ ⋅ ⋅ + an + ⋅ ⋅ ⋅ ,
donde las an son números o funciones dadas por alguna regla o fórmula. Los tres puntos
significan que la serie nunca termina. Si se tiene duda de cómo es la regla usada en la
formación e la serie, el término general o término n-ésimo deberá expresarse, p. ej.
12 + 2 2 + ⋅ ⋅ ⋅ + n 2 + ⋅ ⋅ ⋅
x − x 2 + x
2
+ ⋅ ⋅ ⋅ +
(− 1)n−1 x n
(n − 1)!
+ ⋅ ⋅ ⋅
También usaremos formas abreviadas para denotar las series, p. ej. para las series anteriores, la
forma abreviada será




∞
∑
n=1
∞
∑ n 2
n =1
(− 1)n−1 x n
(n − 1)! .

Las aplicaciones de las series infinitas son muchas, pero mencionamos como lo más importante para
nosotros en este momentos, su uso en la solución de problemas matemáticos que no pueden resolverse
en términos de funciones elementales ( potencias, raíces, funciones trigonométricas y sus inversas,
logaritmos y exponenciales y combinaciones de estos), o en caso de que puedan resolverse, es muy
complicado trabajar con ellos. En estos casos encontramos una respuesta en función de una serie y
usamos
los términos requeridos de acuerdo a la presición deseada. Las ecuaciones diferenciales son
resueltas en muchas ocasiones en función de series infinitas. Una integral definida,
0.1
por ejemplo,
∫ e − x
0
dx , para la cual no hay solución en términos de funciones
elementales, se puede resolver su expandiendo su integrando en una serie e integrando término a
término dicha serie.

4.1.1

Finitas

Una diferencia finita es una expresión matemática de la forma f(x + b) − f(x +a). Si una diferencia finita se divide por b − a se obtiene una expresión similar al cociente diferencial, que difiere en que se emplean cantidades finitas en lugar de infinitesimales. La aproximación de las derivadas por diferencias finitas desempeña un papel central en los métodos de diferencias finitas del análisis numérico para la resolución deecuaciones diferenciales.

La diferencia anterior puede considerarse un operador diferencial que hace corresponder la función f con Δf. El teorema de Taylor puede expresarse por la fórmula

Donde D denota el operador derivada, que hace corresponder con su derivada , es decir,

Formalmente, invirtiendo la exponencial,

Esta fórmula sigue siendo válida en el sentido de que ambos operadores dan el mismo resultado cuando se aplican a un polinomio. Incluso para funciones analíticas, las series de la derecha no convergen con seguridad, sino que puede tratarse de una serie asintótica. Sin embargo, pueden emplearse para obtener aproximaciones más precisas de la derivada. Por ejemplo, Los dos primeros términos de la serie llevan a:

El error de la aproximación es del orden de h².

Las fórmulas análogas para los operadores posterior y central son

4.1.2

Criterio de D'Alembert o Criterio del Cociente (Criterio de la razón)

Sea una serie , tal que a_k > 0 ( serie de términos positivos).

Si existe

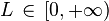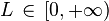con , el Criterio de D'Alembert establece que:

• si L < 1, la serie converge.
• si L > 1, entonces la serie diverge.
• si L = 1, no es posible decir algo sobre el comportamiento de la serie.

En este caso, es necesario probar otro criterio, como el criterio de Raabe.

Criterio de Cauchy (raíz enésima)

Sea una serie , tal que a_k > 0 (serie de términos positivos). Y supongamos que existe

, siendo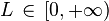

Entonces, si:

• L < 1, la serie es convergente.
• L > 1 entonces la serie es divergente.
• L=1, no podemos concluir nada a priori y tenemos que recurrir al criterio de Raabe, o de comparación, para ver si podemos llegar a alguna conclusión.

4.2 Series Numericas

4.3 Series de Potencias

http://www.unizar.es/analisis_matematico/analisis1/apuntes/09-seriespotencias.pdf

4.4Radio de convergencia

En matemáticas, según el teorema de Cauchy-Hadamard, el radio de convergencia de una serie de la forma , con , viene dado por la expresión:

 Definición

 Si nos limitamos al conjunto de los números reales, una serie de la forma , con , recibe el nombre de serie de potencias centrada en x₀. La serie converge absolutamente para un conjunto de valores de x que verifica que | x − x₀ | < r, donde r es un número real llamado radio de convergencia de la serie. Esta converge, pues, al menos, para los valores de x pertenecientes al intervalo (x₀ − r, x₀ + r), ya que la convergencia para los extremos de este ha de estudiarse aparte, por lo que el intervalo real de convergencia puede ser también semiabierto o cerrado. Si la serie converge solo para x₀, r = 0. Si lo hace para cualquier valor de x, r =.

Ejemplos

Mostraremos el radio de convergencia de algunos desarrollos en series de potencias con sus respectivos radios de convergencia sin justificar porqué el radio de convergencia es el dado.

Radio de convergencia finito

La función 1 / (1 − x) en su desarrollo con centro 0, o sea, en series de potenciax − x₀ = x − 0 = x, tiene el siguiente aspecto:

.

(para el cálculo de la serie vea serie de Taylor). Su radio de convergencia es r = 1. Eso significa que para calcular si tomo cualquier valor cuya distancia al x₀ = 0 es menor que r = 1, por ejemplo el x = 0.25, entonces al remplazarlo en la serie el resultado de calcular la serie será el mismo que remplazarlo en la función, de hecho

.

(la cuenta se puede hacer por serie de potencia). Y por otro lado

.

Pero si tomamos un elemento fuera del radio de convergencia, por ejemplo el x= 2, los más probable es que al remplazarlo en la serie, ésta diverja (por eso el nombre de radio de convergencia). Efectivamente:

.

Distancia a la singularidad

El cálculo del radio de convergencia no es simple. Veamos una función con dos desarrollos en serie con distintos centros y analicemos sus radios de convergencia. La misma función 1 / (1 − x) en su desarrollo con centro x₀ = 3tiene la forma:

.

Pero en este caso su radio de convergencia es r = 2. Notemos que la función 1 / (1 − x) tiene una singularidad en el 1; y que en los dos caso anteriores el radio de convergencia coincide con la distancia del centro a la singularidad: | 0 − 1 | = 1 y | 3 − 1 | = 2. Esto será siempre verdadero para ésta función, pero, no puede generalizarse, como veremos en el siguiente ejemplo:

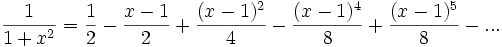
Como no hay singularidades reales podría suponerse que el radio es infinito, sin embargo su radio de convergencia es . Este radio parece caprichoso pero tiene que ver con el hecho de que pasando la función a dominio complejo, existe una singularidad en el denominador.La serie

Radio de convergencia infinito

Por ejempo, la función e^x puede desarrollarse en series de potencia de x − 0 =x, de hecho .

y esto vale para todo real x por eso el radio de convergencia será infinito

4.6 Representacion de Funciones mediante la Serie de Taylor

4.7 Calculo de Integrales Expresadas Como Serie deTaylor

Teorema de Taylor

En cálculo, el teorema de Taylor, recibe su nombre del matemático británico Brook Taylor, quien lo enunció con mayor generalidad en 1712, aunque previamente James Gregory lo había descubierto en 1671. Este teorema permite obtener aproximaciones polinómicas de una función en un entorno de cierto punto en que la función sea diferenciable. Además el teorema permite acotar el error obtenido mediante dicha estimación

Caso de una variable

Este teorema permite aproximar una función derivable en el entorno reducido alrededor de un punto a: E (a, d) mediante unpolinomio cuyos coeficientes dependen de las derivadas de la función en ese punto. Más formalmente, si   ≥ 0 es un entero y   una función que es derivable   veces en el intervalo cerrado [ ,  ] y  +1 veces en el intervalo abierto ( ,  ), entonces se cumple que:¹

(1a)

O en forma compacta

(1b)

Donde   denota el factorial de  , y   es el resto, término que depende de   y es pequeño si   está próximo al punto  . Existen dos expresiones para   que se mencionan a continuación:

(2a)

donde   y  , pertenecen a los números reales,   a los enteros y   es un número real entre   y  :²

(2b)

Si   es expresado de la primera forma, se lo denomina Término complementario de Lagrange, dado que el Teorema de Taylor se expone como una generalización del Teorema del valor medio o Teorema de Lagrange, mientras que la segunda expresión de R muestra al teorema como una generalización del Teorema fundamental del cálculo integral.

Para algunas funciones  , se puede probar que el resto,  , se aproxima a cero cuando   se acerca al ∞; dichas funciones pueden ser expresadas como series de Taylor en un entorno reducido alrededor de un punto   y son denominadas funciones analíticas.

El teorema de Taylor con   expresado de la segunda forma es también válido si la función   tiene números complejos o valores vectoriales. Además existe una variación del teorema de Taylor para funciones con múltiples variables.

[editar]Caso de varias variables

El teorema de Taylor anterior (1) puede generalizarse al caso de varias variables como se explica a continuación. Sea B una bola en R^N centrada en el punto a, y f una función real definida sobre la clausura   cuyas derivadas parciales de orden n+1 son todas continuas en cada punto de la bola. El teorema de Taylor establece que para cualquier  :

Donde la suma se extiende sobre los multi-índices α (esta fórmula usa la notación multi-índice). El resto satisface la desigualdad:

para todo α con |α|=n+1. Tal como sucede en el caso de una variable, el resto puede expresarse explícitamente en términos de derivadas superiores (véase la demostración para los detalles).

[editar]Demostración

Para demostrar el teorema de Taylor para el caso multidimensional, considérese un función   o campo escalar, que suponemos continuo y, para simplificar lo expuesto (aunque una generalización es trivial), de clase  . Sear(t) una función vectorial que va de  , y definamosla cómo  (de ahora en adelante,vse omitirán las flechas de los vectores).Pongamos r(t) = y Ahora hagamos g(t) = f[r(t)] y recordemos que  . Notemos ahora que:

Ahora, derivando sucesivas veces, encontramos que podemos poner de forma muy cómoda:

donde el exponente sobre el gradiente es entendido cómo las sucesivas veces que hacemos el gradiente; es decir,hacemos el producto escalar que está dentro del paréntesis,luego volvemos a derivar otra vez la función, obteniendo otro producto escalar, y así "n" veces. Ahora, empleando el teorema de Taylor para una variable real, expandimos g(t) en su serie de McLaurin:   y haciendo t=1 y sustituyendo las derivadas por las expresiones antes hallada se evidencia que:   Obsérvese que el primer término aparece el gradiente y en el segundo la matriz hessiana, pero escrito con esta notación particular que resulta más cómodo y compacto. La expresión obtenida es equivalente a la expresada más arriba mediante la notación multiíndice.

[editar]Demostración

La demostración de la fórmula (1a), con el resto de la forma (2a), se sigue trivialmente del teorema de Rolle aplicado a la función:

Un cálculo rutinario permite ver la derivada de esta función cumple que:

Se define ahora la función G como:

Es evidente que esta función cumple  , y al ser esta función diferenciable, por el teorema de Rolle se sigue que:

Y como:

Se obtiene finalmente que:

Y substituyendo en esta fórmula la definición de F(a), queda precisamente la fórmula (1a) con la forma del resto (2a).